这样来学习简单多了！用Excel理解梯度下降

本文作者为Jahnavi Mahanta，前American Express（美国运通公司）资深机器学习工程师、深度学习在线教育网站Deeplearningtrack联合创始人。

Jahnavi Mahanta：对算法的作用建立直觉性的理解——在我刚入门机器学习的时候，这让我觉得非常困难。不仅仅是因为理解数学理论和符号本身不容易，也因为它很无聊。我到线上教程里找办法，但里面只有公式或高级别的解释，在大多数情况下并不会深入细节。

就在那时，一名数据科学同事介绍给我一个新办法——用Excel表格来实现算法，该方法让我拍案叫绝。后来，不论是任何算法，我会试着小规模地在 Excel 上学习它——相信我，对于提升你对该算法的理解、完全领会它的数学美感，这个法子简直是奇迹。

案例

让我用一个例子向各位解释。

大多数数据科学算法是优化问题。而这方面最常使用的算法是梯度下降。

或许梯度下降听起来很玄，但读完这篇文章之后，你对它的感觉大概会改变。

这里用住宅价格预测问题作为例子。

现在，有了历史住宅数据，我们需要创建一个模型，给定一个新住宅的面积能预测其价格。

任务：对于一个新房子，给定面积X，价格Y是多少？

让我们从绘制历史住宅数据开始。

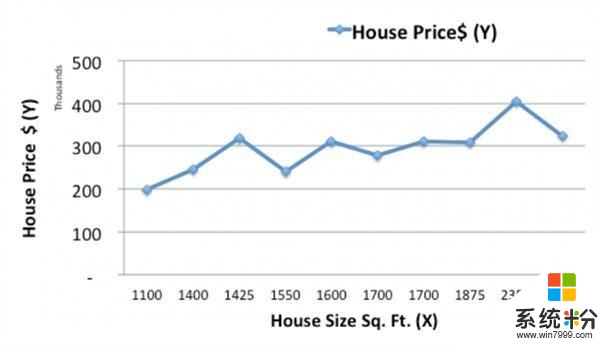
现在，我们会用一个简单的线性模型，用一条线来匹配历史数据，根据面积X来预测新住宅的价格Ypred。

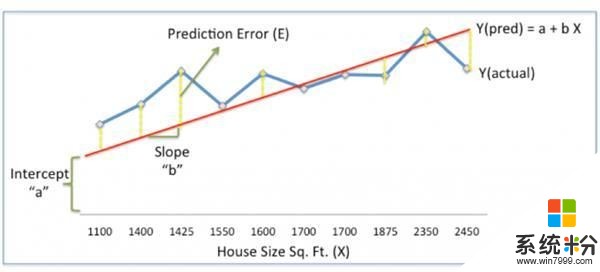
上图中，红线给出了不同面积下的预测价格Ypred。

Ypred = a+bX

蓝线是来自历史数据的实际住宅价格Yactual。

Yactual和Ypred之间的差距，即黄色虚线，是预测误差 E。

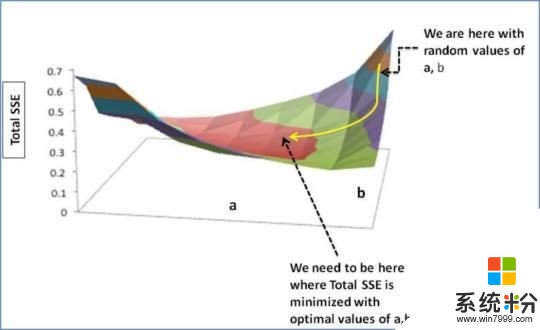
我们需要发现一条使权重a，b获得最优值的直线，通过降低预测误差、提高预测精度，实现对历史数据的最佳匹配。

所以，目标是找到最优a， b，使Yactual和Ypred之间的误差E最小化。

误差的平方和(SSE) = ? a (实际价格 – 预测价格)2=  ? a(Y – Ypred)2

（提醒，请注意衡量误差的方法不止一种，这只是其中一个）

这时便是梯度下降登场的时候。梯度下降是一种优化算法，能找到降低预测误差的最优权重 (a，b) 。 

理解梯度下降

现在，我们一步步来理解梯度下降算法：

用随机值和计算误差（SSE）初始化权重a和b。

计算梯度，即当权重（a & b）从随机初始值发生小幅增减时，SSE的变动。这帮助我们把a & b的值，向着最小化SSE的方向移动。

用梯度调整权重，达到最优值，使SSE最小化。

使用新权重来做预测，计算新SSE。

重复第二、第三步，直到对权重的调整不再能有效降低误差。

我在 Excel 上进行了上述每一步，但在查看之前，我们首先要把数据标准化，因为这让优化过程更快。

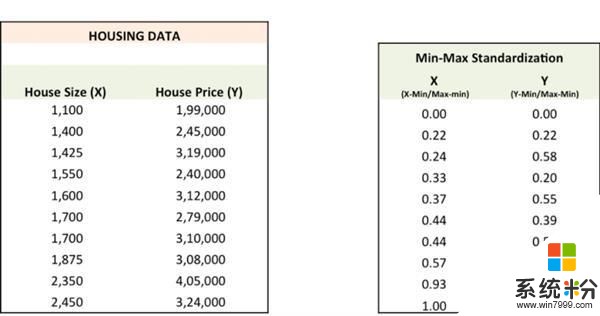
第一步

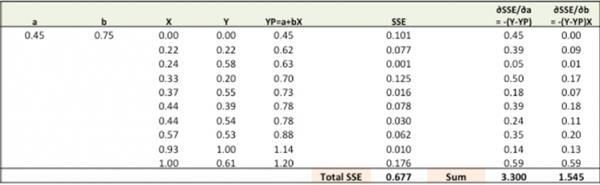
用随机值的a、b初始化直线Ypred = a + b X，计算预测误差SSE。

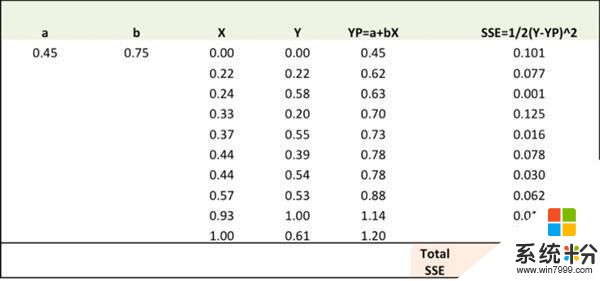
第二步

计算不同权重的误差梯度。

?SSE/?a = – (Y-YP)

?SSE/?b = – (Y-YP)X

这里， SSE=? (Y-YP)2 = ?(Y-(a+bX))2

你需要懂一点微积分，但没有别的要求了。

?SSE/?a、?SSE/?b是梯度，它们基于SSE给出 a、b 移动的方向。

第三步

用梯度调整权重，达到最小化SSE的最优值

我们需要更新a、b的随机值，来让我们朝着最优a、b的方向移动。

更新规则:

a – ?SSE/?a

b – ?SSE/?b

因此：

新的a = a – r * ?SSE/?a = 0.45-0.01*3.300 = 0.42

新的b = b – r * ?SSE/?b= 0.75-0.01*1.545 = 0.73

这里，r是学习率= 0.01， 是权重调整的速率。

第四步

使用新的a、b做预测，计算总的SSE。

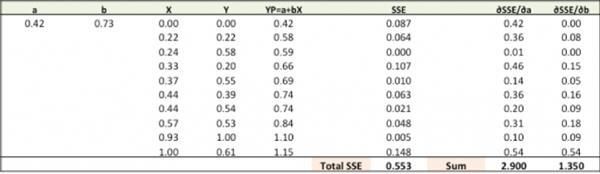
你可以看到，在新预测上 总的SSE从0.677降到了0.553。这意味着预测精度在提升。

第五步

重复第三、第四步直到对 a、b 的调整无法有效降低误差。这时，我们已经达到了最优 a、b，以及最高的预测精度。

这便是梯度下降算法。该优化算法以及它的变种是许多机器学习算法的核心，比如深度网络甚至是深度学习。